|
Mathematical and Computer Simulation Models:
Theory & Application
Scenario 5 - Model Analysis
As a research scientist in the field of aging, you are
aware of the fact that one of the important endpoints of aging research is the “time
of death” of the animals under study.
 This is particularly important if you are
interested in studying any sort of longevity intervention. You have performed
the following laboratory experiment.
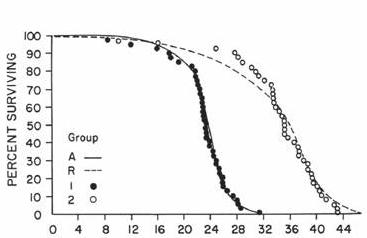
In one area of your laboratory you have
fed 100 rats ad libitum (A in the figure). That is, each rat is allowed to eat as much as it wants, whenever it
wants. In another area of the laboratory, you have set up the same experiment,
the only difference is that you have diet restricted the rats so that they can
only eat a fixed amount of food per day (R in the figure). You compute the
survival curve as illustrated in the above figure and observe that the
restricted group lives significantly longer (12 months or so) than the ad libitum group. This is particularly important if you are
interested in studying any sort of longevity intervention. You have performed
the following laboratory experiment.
In one area of your laboratory you have
fed 100 rats ad libitum (A in the figure). That is, each rat is allowed to eat as much as it wants, whenever it
wants. In another area of the laboratory, you have set up the same experiment,
the only difference is that you have diet restricted the rats so that they can
only eat a fixed amount of food per day (R in the figure). You compute the
survival curve as illustrated in the above figure and observe that the
restricted group lives significantly longer (12 months or so) than the ad libitum group.
You decide to fit a
mathematical survival model to the curves to see if there is any difference or
if it is just an experimental fluke. The results of your work seem to indicate
that there is really a diet-related effect. However, you are not sure and want
to rerun the experiment. On the other hand, it is extremely costly to run such
experiments so you cannot run too many repeats or too large a sample size. What
do you do?
Back to main Scenario page continue
|

